Union By Rank and Path Compression in Union-Find (Disjoint Sets)

Disjoint Set: no element belongs to more than one set.

A union-find structure maintains a collection of disjoined set.

It supports two O(log n) time operations:

Unite – Joins two sets.
Find – finds the representative of the set that contains a given element.

In a union-find structure, one element in each set is the representative of the set, and there is a path from any other element of the set to the representative.

Fig. 1

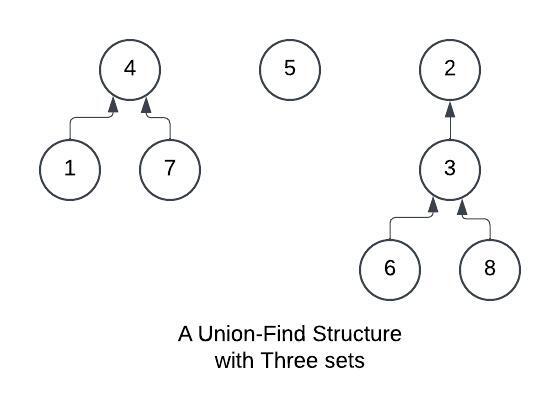
For example: Assume that the sets are {1, 4, 7}, {5} and {2, 3, 6, 8}.

Fig. 1 shows one way to represent these sets.

In this case, the representatives of the sets are 4, 5 and 2.

We can find the representative of any element by following the path that begins at the element.

For example, the element 2 is the representative of the element 6, because we follow the path 6-> 3-> 2.

Two elements belong to the same set exactly when their representatives are the same.

Fig. 2

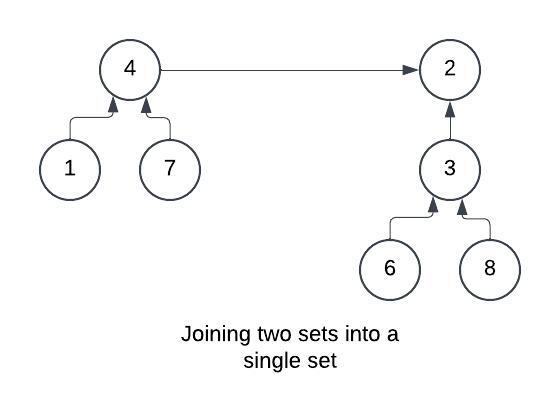
To join two sets, the representative of one set is connected to the representative of another set.

For example, Fig 2 shows a possible way to join the sets {1,4,7} and {2,3,6,8}.

From this on, the element 2 is the representative for the set and the old representative 4 points to the element 2.

The efficiency of the union find structure depends on how the sets are joined.

Joining to Sets:

We can follow a simple strategy:

Always connect to the representative of smaller set to the representative of the larger set.

(Or If the sets are of equal size, we can make an arbitrary choice).

Using this strategy the length of the path will be O(log n), So we can find the representative of any element efficiently by following the corresponding path.

Implementation: The union-find structure can be conveniently implemented using arrays.

In the following implementation, the array link indicates for each element the next element in the path or the element itself if it is a representative,

and the array size indicates for each representative the size of the corresponding set.

for(int i=1; i <= n; i++) link[i] = i;

for(int i=1; i <= n; i++) size[i] = 1;

The function find returns the representative for an element x.

The representative can be found by following the path that begins at x.

int find(int x){
	while( x != link[x]){
        x = link[x];
    } 
    return x;
}

The function same checks whether elements a and b belong to the same set.

This can easily be done by using this function find:

boolean same(int a, int b){
    return find(a) == find(b);
}

The function unite joins the sets that contain elements a and b ( the elements have to be in different sets).

The function first finds the representatives of the sets and then connects the smaller set to the larger set.

c++ version

void unite(int a, int b) {
    a = find(a);
    b = find(b);
    if (size[a] < size[b]) 
        swap(a, b);
    size[a] += size[b];
    link[b] = a;            
}

Java Version

void unite(int a, int b) {
    a = find(a);
    b = find(b);

    if (a != b) {
        if (size[a] < size[b]) {
            int temp = a;
            a = b;
            b = temp;
        }

        parent[b] = a;
        size[a] += size[b];
        //size[b] = 0;
    }
}

The time complexity of the function find is O(log n) assuming that the length of each path is O(log n).

In this case, the function same and unite also work on O(log n) time.

The function unite makes sure that the length of each path is O(log n) by connecting the smaller set to the larger set.

Here is an alternative way to implement the find operation:

int find(int x) {
    If(x == link[x]) 
    return x;

    linx[x] = find(link[x]);

    return link[x];
}

The function uses path compression: each element in the path will directly point to its representative after the operation.

The union-find function with path compression works almost a constant time.

However, path compression cannot be used in some applications of the union-find structure, such as in the dynamic connectivity algorithm.

Reference: Guide to Competitive Programming

Union by Rank and Path Compression:

public class DisjointSet {
    private int[] parent;
    private int[] rank;
    
    public DisjointSet(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
            rank[i] = 0;
        }
    }
    
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // Path compression
        }
        return parent[x];
    }
    
    public void union(int x, int y) {
        int p1 = find(x);
        int p2 = find(y);
        
        if (p1 != p2) {
            if (rank[p1] > rank[p2]) {
                parent[p2] = p1;
            } else if (rank[p1] < rank[p2]) {
                parent[p1] = p2;
            } else {
                parent[p2] = p1;
                rank[p1]++;
            }
        }
    }
}

Using array parent, size and rank

private static void union(int x, int y){
        int p1 = find(x);
        int p2 = find(y);

        if(p1 != p2){
            if(rank[p1] >= rank[p2]){
                parent[p2] = p1;
                size[p1] += size[p2];
                size[p2] =0;
                if(rank[p1] == rank[p2]){
                    rank[p1]++;
                }

            }
            else{
                parent[p1] = p2;
                size[p2] += size[p1];
                size[p1]=0;
            }
        }

}