Depth-First Search Breadth-First Search Union Find Graph

Leetcode Link for Number of Provinces

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

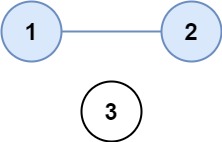
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]

Output: 2

Example 2:

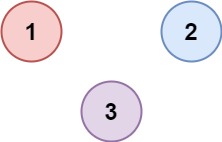
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]

Output: 3

Constraints:

  • 1 <= n <= 200
  • n == isConnected.length
  • n == isConnected[i].length
  • isConnected[i][j] is 1 or 0.
  • isConnected[i][i] == 1
  • isConnected[i][j] == isConnected[j][i]

We will use three different approaches to solve this problem:

1. Union Find (Disjoint Set)

2. Depth First Search

3. Breadth First Search

Union Find (Disjoint Set):

We will be doing it in two steps:

- 1. Write a class DisjointSet

- 2. Use the unite and getProvinceCout() method from the findCrileNum() method

If you need to brush up your knowledge about disjoint set, below is the link:

Union By Rank and Path Compression in Union-Find (Disjoint Sets)

Implementation using Union Find (Disjoint Set):


package com.spsoft.leetcode.medium.graph;

public class L547NumberOfProvinces_DisjointSet {
    DisjointSet ds;
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        ds = new DisjointSet(n);
        for(int i=0; i < n; i++){
            for(int j=i+1; j < n; j++){
                if(isConnected[i][j] == 1)
                    ds.unite(i, j);
            }
        }
        return ds.getProvinceCount(n);
    }

    private class DisjointSet{
        int n;
        int count=0;
        int [] parent;
        int [] rank;
        public DisjointSet(int n){
            this.n = n;
            parent = new int[n];
            rank = new int[n];

            for(int i=0; i < n; i++){
                parent[i] = i;
            }
        }

        int find(int x){
            if(x != parent[x]){
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }

        void unite(int u, int v){
            int i = find(u);
            int j = find(v);
            if(i == j)
                return;
            if(rank[i] >= rank[j]){
                parent[j] = i;
                if(rank[i] == rank[j])
                    rank[i]++;
            }
            else {
                parent[i] = j;
            }
        }

        int getProvinceCount(int n){
            for(int i= 0; i < n; i++){
                if(parent[i]==i)
                    count++;
            }
            return count;
        }

    }
}

Github Link for Union Find

Implementation using DFS and BFS:


package com.spsoft.leetcode.medium.graph;

import java.util.*;

public class L547NumberOfProvinces_DFS_BFS {
    boolean[] visited;

    public int findCircleNum(int[][] isConnected) {
        int count = 0;
        int n = isConnected.length;
        visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                count++;
                dfs(i, n, isConnected);
                //bfs(i, n, isConnected);
            }
        }
        return count;
    }

    void dfs(int i, int n, int[][] isConnected) {
        visited[i] = true;
        for (int j = 0; j < n; j++) {
            if (!visited[j] && isConnected[i][j] == 1) {
                dfs(j, n, isConnected);
            }
        }
    }

    void bfs(int city, int n, int[][] isConnected) {
        Queue<Integer> q = new ArrayDeque<>();
        visited[city] = true;
        q.offer(city);
        while (!q.isEmpty()) {
            Integer u = q.poll();
            for (int v = 0; v < n; v++) {
                if (!visited[v] && isConnected[u][v] == 1) {
                    visited[v] = true;
                    q.offer(v);
                }
            }

        }
    }
}

Github Link for DFS and BFS

Time and Space Complexity:

  • Disjoint Set (Union-Find):

    • Time Complexity: 𝑂(𝑛2. 𝛼(𝑛))

      Union-Find operations (find and unite) are nearly constant time 𝑂(𝛼(𝑛)),

      where 𝛼 is the inverse Ackermann function, very slowly growing. Each edge is processed once, leading to 𝑂(𝑛2 .𝛼(𝑛)) complexity.

    • Space Complexity: 𝑂(𝑛)

      Memory is used for the parent and rank arrays, both of size 𝑛.

  • DFS (Depth-First Search):

    • Time Complexity: 𝑂(𝑛2)

    The DFS function is called once for each node. Each call processes every edge connected to the node, resulting in an 𝑂(𝑛2) complexity overall.

    • Space Complexity: 𝑂(𝑛) , due to the recursion stack and the visited array of size 𝑛.

  • BFS (Breadth-First Search):

    • Time Complexity: 𝑂(𝑛2)

      Similar to DFS, BFS processes each node and its edges, leading to an 𝑂(𝑛2) complexity.

    • Space Complexity: 𝑂(𝑛),

      Memory is required for the visited array and the queue, holding up to 𝑛 nodes in the worst case.

Comparative Summary:

Time Complexity Comparison:

  • Union-Find: 𝑂(𝑛2. 𝛼(𝑛))

  • DFS: 𝑂(𝑛2)

  • BFS: 𝑂(𝑛2)

While DFS and BFS have straightforward 𝑂(𝑛2) time complexity,

the Union-Find approach is slightly more efficient in practice due to the near-constant time complexity of its operations.

Space Complexity Comparison:

All three methods have linear space complexity 𝑂(𝑛).

Author: Mohammad J Iqbal

Mohammad J Iqbal

Follow Mohammad J Iqbal on LinkedIn