Leetcode 200 - Number of Islands
| Array | Depth First Search | Breadth First Search | Union Find | Matrix |
Leetcode Link for Number of Islands
Given an m x n 2D binary grid grid which represents a map of ‘1’s (land) and ‘0’s (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1
Example 2:
Input: grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3
Example 3:
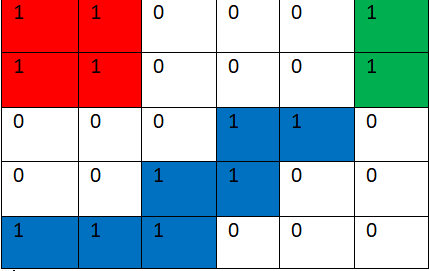
Output: 3
Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 300
- grid[i][j] is ‘0’ or ‘1’.
Solution:
Key Components:
Define Moves : A 2D array representing possible movements (left, right, up, down)
private static final int[][] moves = {
{0, -1}, // left
{0, 1}, // right
{-1, 0}, // up
{1, 0} // down
};
numIslands Method:
public int numIslands(char[][] grid) {
int count = 0;
int m = grid.length;
int n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
bfs(grid, i, j, m, n);
// Or use dfs(grid, i, j, m, n);
count++;
}
}
}
return count;
}
-
Purpose: This method initiates the counting of islands in the grid.
-
Process:
-
Iterates through each cell in the grid.
-
If a cell is ‘1’, it triggers a call to bfs (or dfs), marking the entire island as visited, and increments the island count.
-
dfs method:
private void dfs(char[][] grid, int i, int j, int m, int n) {
if ((i < 0 || i >= m) || (j < 0 || j >= n))
return;
if (grid[i][j] == '0')
return;
grid[i][j] = '0'; // mark as visited
for (int[] move : moves) {
dfs(grid, i + move[0], j + move[1], m, n);
}
}
-
Purpose: Recursively marks all connected ‘1’s (land) as ‘0’s (visited).
-
Process:
- Checks if the current cell is out of bounds or water.
- Marks the current cell as visited.
- Recursively calls itself for all four possible directions.
bfs method:
private void bfs(char[][] grid, int i, int j, int m, int n) {
Deque<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{i, j});
grid[i][j] = '0'; // mark as visited
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0];
int y = cell[1];
for (int[] move : moves) {
int x1 = x + move[0];
int y1 = y + move[1];
if ((x1 >= 0 && x1 < m) && (y1 >= 0 && y1 < n) && grid[x1][y1] == '1') {
queue.add(new int[]{x1, y1});
grid[x1][y1] = '0'; // mark as visited
}
}
}
}
Github Link: https://github.com/miqbal3636/problem_solving/blob/main/src/com/spsoft/leetcode/medium/matrix/L200NumberOfIslands.java
-
Purpose: Uses a queue to iteratively mark all connected ‘1’s (land) as ‘0’s (visited).
-
Process:
-
Adds the starting cell to the queue and marks it as visited.
-
Continues processing each cell in the queue, marking all reachable land cells as visited.
-
All Together:
public class Solution {
private static final int[][] moves = {
{0, -1}, // left
{0, 1}, // right
{-1, 0}, // up
{1, 0} // down
};
public int numIslands(char[][] grid) {
int count = 0;
int m = grid.length;
int n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
bfs(grid, i, j, m, n);
//dfs(grid,i,j,m,n);
count++;
}
}
}
return count;
}
private void dfs(char[][] grid, int i, int j, int m, int n) {
if ((i < 0 || i >= m) || (j < 0 || j >= n))
return;
if (grid[i][j] == '0')
return;
// mark as visited
grid[i][j] = '0';
for (int[] move : moves) {
dfs(grid, i + move[0], j + move[1], m, n);
}
}
private void bfs(char[][] grid, int i, int j, int m, int n) {
Deque<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{i, j});
grid[i][j] = '0'; // mark as visited
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0];
int y = cell[1];
for (int[] move : moves) {
int x1 = x + move[0];
int y1 = y + move[1];
if ((x1 >= 0 && x1 < m) && (y1 >= 0 && y1 < n) && grid[x1][y1] == '1') {
queue.add(new int[]{x1, y1});
grid[x1][y1] = '0'; // mark as visited
}
}
}
}
}
Time Complexity for Both BFS and DFS:
In both BFS and DFS, we visit each cell in the grid exactly once:
Number of Operations: Each cell in the grid is processed for a constant amount of work (marking it as visited and handling its neighbors).
Total Cells: In the worst-case scenario, we might need to visit every cell which is M * N (where M is the number of rows and N is the number of columns).
Therefore, the time complexity for both BFS and DFS is O(M * N).
Space Complexity for DFS:
DFS uses a recursive stack that can go as deep as the largest island:
Recursive Stack Depth: In the worst case, the recursive call depth can go up to the size of the largest island, which again can be O(M * N) if it’s very fragmented.
Auxiliary Space: Beyond the recursion stack, there’s no significant additional space needed.
Space Complexity for BFS:
BFS uses a queue to keep track of the cells that need to be processed:
Queue Size: In the worst case, the queue can hold up to all the cells of the largest island. This means the queue’s size can go up to O(M * N) in the worst case.
The space complexity of BFS could sometimes be argued as O(min(M, N)), depending on how we interpret the queue’s behavior.
- Scenario: Space Complexity O(min(M, N))
In some descriptions of BFS, the space complexity can be considered O(min(M, N)) based on the following:
Grid Dimensions: Typically, the longest possible contiguous line of ‘1’s (either row-wise or column-wise) determines the depth or size of the queue.
Worst Case Interpretation: In a less fragmented scenario where the island shapes are such that the queue never stores more than the shortest dimension of the grid, the queue size might hover around the minimum of rows or columns.
To see it in action:
Rectangular Grid (Dense Island): If an island’s spread is more along the shorter side (say columns for a vertical strip or rows for a horizontal strip), the BFS queue might alternatively store something around O(min(M, N)) elements.
- Space Complexity O(M * N) in Practicality
However, in a fragmented grid with numerous small islands, or one massive, complex island, the queue can grow significantly, often reaching sizes closer to O(M * N) in extreme cases.
Auxiliary Space: Additional space is used for storing pointers, counters, etc., but this is negligible compared to the queue.
Summary:
While the theoretical underpinning is strong for O(min(M, N)), the practical viewpoint generally sticks to O(M * N) to cover all possible worst-case scenarios, especially with complex or highly fragmented islands.
Summary
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| BFS | O(M * N) | O(M * N) |
| DFS | O(M * N) | O(M * N) |
Both BFS and DFS exhibit the same time and space complexity in the worst case, making them equally efficient for this problem.
Author: Mohammad J Iqbal
