HackerRank - Roads and Libraries using the Union Find (Disjoint Sets) data structure
| Union Find (Disjoint Sets) | Graph Theory |
Problem Link on HackerRank: Roads and Libraries
In this post, I cover:
-
Understanding the Roads and Libraries problem
-
Implementing Union Find with Union by Size and Rank
-
Optimizing with path compression
-
Step-by-step code walkthroughs
If you are not familiar with Union Find (Disjoint Sets), you can read the article below:
Union By Rank and Path Compression in Union-Find (Disjoint Sets)
Problem Description: Determine the minimum cost to provide library access to all citizens of HackerLand. There are cities numbered from to . Currently there are no libraries and the cities are not connected. Bidirectional roads may be built between any city pair listed in . A citizen has access to a library if:
Their city contains a library. They can travel by road from their city to a city containing a library. Example
The following figure is a sample map of HackerLand where the dotted lines denote possible roads:
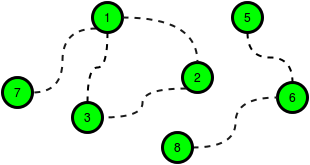
c_road = 2
c_lib = 3
cities = [[1,7],[1,3],[1,2],[2,3],[5,6],[6,8]]
The cost of building any road is c_road = 2, and the cost to build a library in any city is c_lib = 3. Build 5 roads at a cost of 5 * 2 = 10 and 2 libraries for a cost of 6. One of the available roads in the cycle
1 - > 2 -> 3 -> 1 is not necessary.
There are queries, where each query consists of a map of HackerLand and value of c_lib and c_road. For each query, find the minimum cost to make libraries accessible to all the citizens.
Function Description:
Complete the function roadsAndLibraries in the editor below. roadsAndLibraries has the following parameters:
-
int n: integer, the number of cities
-
int c_lib: integer, the cost to build a library
-
int c_road: integer, the cost to repair a road
-
int cities[m][2]: each contains two integers that represent cities that can be connected by a new road
Returns
- int: the minimal cost
Input Format:
The first line contains a single integer q, that denotes the number of queries.
The subsequent lines describe each query in the following format:
- The first line contains four space-separated integers that describe the respective values of n, m , c_lib and c_road, the number of cities, number of roads, cost of a library and cost of a road.
- Each of the next lines contains two space-separated integers, u[i] and v[i], that describe a bidirectional road that can be built to connect cities u[i] and v[i].
Constraints:
- 1 <= q <= 10
- 1 <= n <= 105
- 0 <= m <= min(105, n(n-1)/2)
- 1 <= c_road, c_lib <= 105
- 1 <= u[i],v[i] <= n
- Each road connects two distinct cities.
Sample Input:
STDIN Function
----- --------
2 q = 2
3 3 2 1 n = 3, cities[] size m = 3, c_lib = 2, c_road = 1
1 2 cities = [[1, 2], [3, 1], [2, 3]]
3 1
2 3
6 6 2 5 n = 6, cities[] size m = 6, c_lib = 2, c_road = 5
1 3 cities = [[1, 3], [3, 4],...]
3 4
2 4
1 2
2 3
5 6
Sample Output
4
12
Explanation
Perform the following q=2 queries:
- HackerLand contains n=3 cities and can be connected by m=3 bidirectional roads. The price of building a library is c_lib=2 and the price for repairing a road is c_road = 1.
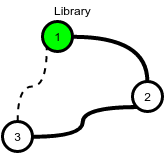
The cheapest way to make libraries accessible to all is to:
- Build a library in city 1 at a cost of x=2.
- Build the road between cities 1 and 2 at a cost of y=1
- Build the road between cities 2 and 3 at a cost of y=1.
This gives a total cost of 2+1+1=4. Note that the road between cities 3 and 1 does not need to be built because each is connected to city 2.
- In this scenario it is optimal to build a library in each city because the cost to build a library is less than the cost to build a road.
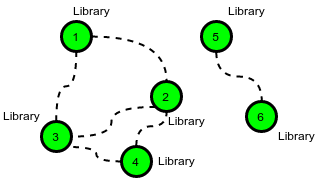
There are 6 cities, so the total cost is: 6 * 2 = 12.
Implementation:
DisjointSet class:
The DisjointSet class implements the Union-Find algorithm, which is a data structure used to efficiently manage and merge disjoint sets. This class is particularly useful for solving problems involving connected components.
Key features of the DisjointSet class include:
-
Initialization: The constructor initializes arrays for parent, rank, and size. Each element starts as its own parent, representing a distinct set.
-
Find Operation: The find method utilizes path compression to find the representative (parent) of a set, ensuring a more efficient lookup.
-
Union Operation: The unite method merges two sets, taking into account the rank of each set to maintain a balanced structure. This helps keep the tree height low, resulting in faster operations.
-
Counting Groups: The numGroupsCount method counts the number of distinct groups, calculates the total number of roads, and connected cities within the network.
private static class DisjointSet {
int[] parent;
int[] rank;
int[] size;
long count = 0;
long totalRoads = 0;
long totalConnectedCities = 0;
public DisjointSet(int n) {
parent = new int[n + 1];
rank = new int[n + 1];
size = new int[n + 1];
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]); // Path compression
}
return parent[x];
}
void unite(int u, int v) {
int i = find(u);
int j = find(v);
if (i == j)
return;
if (rank[i] >= rank[j]) {
parent[j] = i;
size[i] += size[j];
if (rank[i] == rank[j])
rank[i]++;
} else {
parent[i] = j;
size[j] += size[i];
}
}
long numGroupsCount(int n) {
for (int i = 1; i <= n; i++) {
if (parent[i] == i) {
count++;
totalRoads += size[i] - 1;
totalConnectedCities += size[i];
}
}
return count;
}
}
}
roadsAndLibraries method:
The roadsAndLibraries method calculates the minimum cost of ensuring every city has access to a library, either by building libraries directly in the cities or by constructing roads to connect cities that share a single library.
Key features of the roadsAndLibraries method include:
-
Initialization: A DisjointSet object is created to manage the sets of connected cities.
-
Cost Comparison: If the cost of building a library (c_lib) is less than or equal to the cost of building a road (c_road), the method returns the total cost of building a library in every city.
-
Processing Connections: Each city connection is processed using the unite method of the DisjointSet class to group connected cities.
-
Counting Groups and Cities: The numGroupsCount method of the DisjointSet class is called to count the number of connected groups and the total number of connected cities.
-
Calculating Isolated Cities: The number of isolated cities is determined by subtracting the total number of connected cities from the total number of cities (n).
-
Total Cost Calculation: The total cost is calculated by considering the cost of building libraries in the connected groups, isolated cities, and the cost of constructing roads between connected cities.
public static long roadsAndLibraries(int n, int c_lib, int c_road, List<List<Integer>> cities) {
DisjointSet ds = new DisjointSet(n);
// Build one library in each city if the cost of building a library is less than building a road
if (c_lib <= c_road) {
return (long) c_lib * n;
}
// Process each city connection
for (List<Integer> edge : cities) {
ds.unite(edge.get(0), edge.get(1)); // No adjustment needed for 1-based indexing
}
// Calculate the number of connected groups and total connected cities
long numConnectedGroups = ds.numGroupsCount(n);
long totalConnectedCities = ds.totalConnectedCities;
// Calculate the number of isolated cities
long numIsolatedCities = n - totalConnectedCities;
// Calculate the total cost
return (long) (numConnectedGroups * c_lib) + (long) (numIsolatedCities * c_lib) + (long) (ds.totalRoads * c_road);
}
Driver (main) Method:
This main method is provided by HackerRank to capture input, call method roadsAndLibraries and write output:
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bufferedWriter = new BufferedWriter(new FileWriter(System.getenv("OUTPUT_PATH")));
int q = Integer.parseInt(bufferedReader.readLine().trim());
IntStream.range(0, q).forEach(qItr -> {
try {
String[] firstMultipleInput = bufferedReader.readLine().replaceAll("\\s+$", "").split(" ");
int n = Integer.parseInt(firstMultipleInput[0]);
int m = Integer.parseInt(firstMultipleInput[1]);
int c_lib = Integer.parseInt(firstMultipleInput[2]);
int c_road = Integer.parseInt(firstMultipleInput[3]);
List<List<Integer>> cities = new ArrayList<>();
IntStream.range(0, m).forEach(i -> {
try {
cities.add(
Stream.of(bufferedReader.readLine().replaceAll("\\s+$", "").split(" "))
.map(Integer::parseInt)
.collect(toList())
);
} catch (IOException ex) {
throw new RuntimeException(ex);
}
});
long result = Result.roadsAndLibraries(n, c_lib, c_road, cities);
bufferedWriter.write(String.valueOf(result));
bufferedWriter.newLine();
} catch (IOException ex) {
throw new RuntimeException(ex);
}
});
bufferedReader.close();
bufferedWriter.close();
}
Time and Space Complexity Analysis:
The time complexity of the Union-Find algorithm with path compression and union by rank is amortized nearly constant time. Specifically, it’s O(α(n)), where α is the inverse Ackermann function, which grows very slowly.
However, since we are processing each of the cities array with n elements, the overall time complexity can be considered as O(m α(n)), where m is the number of edges (connections between cities).
Here’s the breakdown: - Union-Find operations (find and unite): O(α(n)) for each operation. Processing all edges: If m is the number of edges, and we perform Union-Find for each, it will be O(m * α(n)).
Space Complexity: O(n) as we are using arrays parent, rank and size all having n.
GitHub Link for full source code
Author: Mohammad J Iqbal

Follow Mohammad J Iqbal on LinkedIn
Join the LinkedIn group Algorithm Avengers to share thoughts and learn about Problem Solving, Data Structures, and Algorithms.