Leetcode 733 - Flood Fill
| Array | Depth First Search | Breadth First Search | Matrix |
You are given an image represented by an m x n grid of integers image, where image[i][j] represents the pixel value of the image. You are also given three integers sr, sc, and color. Your task is to perform a flood fill on the image starting from the pixel image[sr][sc].
To perform a flood fill:
-
Begin with the starting pixel and change its color to color.
-
Perform the same process for each pixel that is directly adjacent (pixels that share a side with the original pixel, either horizontally or vertically) and shares the same color as the starting pixel.
-
Keep repeating this process by checking neighboring pixels of the updated pixels and modifying their color if it matches the original color of the starting pixel.
-
The process stops when there are no more adjacent pixels of the original color to update.
Return the modified image after performing the flood fill.
Example 1:
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation:
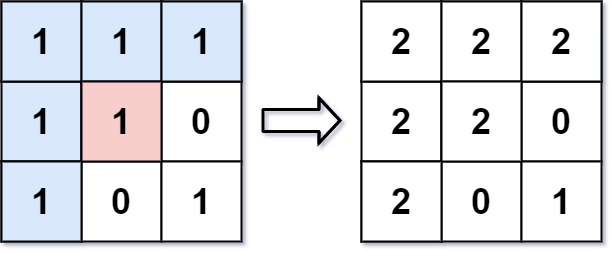
Image Credit: Leetcode
From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not horizontally or vertically connected to the starting pixel.
Example 2:
Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation:
The starting pixel is already colored with 0, which is the same as the target color. Therefore, no changes are made to the image.
Constraints:
- m == image.length
- n == image[i].length
- 1 <= m, n <= 50
- 0 <= image[i][j], color < 216
- 0 <= sr < m
- 0 <= sc < n
Solution:
floodFill Method:
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
int srcColor = image[sr][sc];
if(srcColor != color){
floodFillHelper(image,sr, sc, srcColor, color);
}
return image;
}
-
Purpose: This is the main method that initiates the flood fill process.
-
Parameters:
-
image: A 2D array representing the image.
-
sr: Starting row index for the flood fill.
-
sc: Starting column index for the flood fill.
-
color: The new color to apply.
-
-
Process:
-
It first checks the color of the starting pixel.
-
If the start color (srcColor) is different from the new color (color), it calls the helper function to fill in the new color.
-
The function returns the modified image array.
-
floodFillHelper Method:
public void floodFillHelper(int[][] image, int sr, int sc, int srcColor, int targetColor){
if((sr < 0 || sr >= image.length) || (sc < 0 || sc >= image[0].length) || (image[sr][sc] != srcColor) || (image[sr][sc] == targetColor))
return;
image[sr][sc] = targetColor;
floodFillHelper(image, sr -1, sc, srcColor, targetColor);
floodFillHelper(image, sr +1, sc, srcColor, targetColor);
floodFillHelper(image, sr , sc -1, srcColor, targetColor);
floodFillHelper(image, sr, sc + 1, srcColor, targetColor);
}
Github Link: https://github.com/miqbal3636/problem_solving/blob/main/src/com/spsoft/leetcode/easy/matrix/L733FloodFill.java
-
Purpose: This helper method carries out the actual flood filling using a recursive approach.
-
Parameters:
-
image: A 2D array representing the image.
-
sr: Current row index.
-
sc: Current column index.
-
srcColor: The initial color that needs to be replaced.
-
targetColor: The new color to apply.
-
-
Process:
-
Base Case: The function has several base cases to stop recursion:
-
If the current pixel is out of bounds (either row or column is out of the valid range).
-
If the current pixel’s color is not the srcColor (ensuring it only fills adjacent pixels of the same original color).
-
If the current pixel is already the targetColor.
-
Recursive Step: If none of the base cases are met, it:
-
Changes the current pixel’s color to the targetColor.
-
Calls itself recursively for the top, bottom, left, and right neighboring pixels.
-
This approach ensures that the flood fill algorithm effectively and efficiently fills the region surrounding the starting pixel with the new color.
All Together:
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
int srcColor = image[sr][sc];
if(srcColor != color){
floodFillHelper(image,sr, sc, srcColor, color);
}
return image;
}
public void floodFillHelper(int [][] image, int sr, int sc, int srcColor, int targetColor){
if((sr < 0 || sr >= image.length) || (sc < 0 || sc >= image[0].length) || (image[sr][sc] != srcColor) || (image[sr][sc] == targetColor))
return;
image[sr][sc] = targetColor;
floodFillHelper(image, sr -1, sc, srcColor, targetColor);
floodFillHelper(image, sr +1, sc, srcColor, targetColor);
floodFillHelper(image, sr , sc -1, srcColor, targetColor);
floodFillHelper(image, sr, sc + 1, srcColor, targetColor);
}
}
Time Complexity:
The flood fill algorithm, as implemented with the floodFillHelper method, examines each pixel in the region exactly once. Here’s the breakdown:
-
Number of Recursive Calls: In the worst case, the algorithm will visit all M * N pixels in the image, where M is the height (number of rows) and N is the width (number of columns) of the image.
-
Operations per Pixel: Each pixel requires a constant amount of work (changing the color and making up to 4 recursive calls).
Therefore, the time complexity is O(M * N), where M is the number of rows and N is the number of columns.
Space Complexity:
The space complexity depends on the space required for the recursion stack. In the worst-case scenario (where the entire image needs to be filled or the recursive calls are limited to a single line):
-
Recursive Depth: The maximum depth of the recursion stack will be the maximum of M or N if the fill spreads in one direction.
-
Auxiliary Space: We don’t use any additional data structures apart from the recursion stack.
Therefore, the space complexity in the worst case is O(M * N) (recursive depth - total number of pixels if the fill is very fragmented), and in the average case, it’s more realistically O(max(M, N)) (depth of the longest path).
Author: Mohammad J Iqbal
