Leetcode 102 - Binary Tree Level Order Traversal
| Tree | Binary Tree | Breadth First Search |
Leetcode Link for Binary Tree Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes’ values. (i.e., from left to right, level by level).
Example 1:
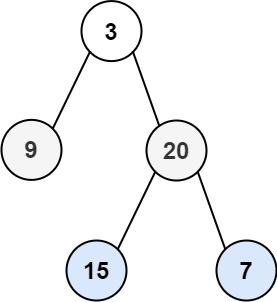
Image Credit: Leetcode
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
Constraints:
-
The number of nodes in the tree is in the range [0, 2000].
-
-1000 <= Node.val <= 1000
Solution:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null)
return result;
Deque<TreeNode> q = new ArrayDeque<>();
q.add(root);
while (!q.isEmpty()) {
List<Integer> currentLevel = new ArrayList<>();
for (int i = q.size(); i > 0; i--) {
TreeNode node = q.poll();
currentLevel.add(node.val);
TreeNode left = node.left;
TreeNode right = node.right;
if (left != null)
q.offer(left);
if (right != null)
q.offer(right);
}
result.add(currentLevel);
}
return result;
}
Github Link: https://github.com/miqbal3636/problem_solving/blob/main/src/com/spsoft/leetcode/medium/bfs/L102BinaryTreeLevelOrderTraversal.java
Explanation:
1. Initialization:
An empty list result is created to store the final list of levels.
If root is null, an empty result list is returned.
2. Queue Setup:
A Deque (double-ended queue) q is initialized and the root node is added to it. This queue helps in processing nodes level by level.
3. Level Traversal:
A while loop runs as long as the queue is not empty.
Within the loop, a new list currentLevel is created to hold the values of nodes at the current level.
A for loop iterates over the nodes at the current level (the size of the queue before processing the level).
4. Processing Nodes:
Nodes are removed (polled) from the front of the queue and their values are added to currentLevel.
If the node has a left child, it’s added (offered) to the queue.
Similarly, if the node has a right child, it’s also added to the queue.
Add Current Level to Result:
Once all nodes at the current level are processed, currentLevel is added to result.
5. Return Result:
After processing all levels, the result list containing lists of node values at each level is returned.
This implementation ensures that nodes are traversed level by level.
Time Complexity: O(n), where n is the number of nodes in the tree.
Space Complexity: The space complexity is also O(n) due to the storage required for the result list and the queue.
Author: Mohammad J Iqbal
